矩阵微分简记

符号约定

本文所涉及的向量、矩阵及函数皆为实值向量、矩阵和函数

$\pmb{x}=\left[x_1, x_2, \cdots, x_m\right]^\mathrm{T}\in \mathbb{R}^m$，即默认为$m\times 1$列向量

$\pmb{X}=\left[\pmb{x}_1,\pmb{x}_2,\cdots,\pmb{x}_n\right]\in \mathbb{R}^{m\times n}$，即默认为$m\times n$矩阵

函数符号约定如下：

函数类型	自变量为向量$\pmb{x}\in \mathbb{R}^m$	自变量为矩阵$\pmb{X}\in \mathbb{R}^{m\times n}$
标量函数$f\in \mathbb{R}$	$f(\pmb{x})$	$f(\pmb{X})$
向量函数$\pmb{f}\in \mathbb{R}^p$	$\pmb{f}(\pmb{x})$	$\pmb{f}(\pmb{X})$
矩阵函数$\pmb{F}\in \mathbb{R}^{p\times q}$	$\pmb{F}(\pmb{x})$	$\pmb{F}(\pmb{X})$

两种布局

矩阵求导比较复杂的部分就在于哪个分量要对哪个分量求导，并且求完导后的结果按照什么形式排布。下面介绍两种布局方式。

Jacobian矩阵

标量对向量求导

将$1\times m$行向量偏导算子记为

$$\mathrm{D}_{\pmb{x}}\overset{\mathrm{def}}{=}\frac{\partial}{\partial \pmb{x}^\mathrm{T}}=\left[\frac{\partial}{\partial x_1},\cdots,\frac{\partial}{\partial x_m}\right]$$

于是，可以给出实值标量函数对$\pmb{x}$的偏导向量

$$\mathrm{D}_{\pmb{x}}f(\pmb{x})=\frac{\partial f(\pmb{x})}{\partial \pmb{x}^\mathrm{T}}=\left[\frac{\partial f(\pmb{x})}{\partial x_1},\cdots,\frac{\partial f(\pmb{x})}{\partial x_m}\right]$$

注意，在这种定义下，我们对分母进行了转置，求导得到的结果也是行向量。

标量对矩阵求导

当变元是矩阵的时候，仿照上述定义，比较直观地给出下面的定义

$$\mathrm{D}_{\pmb{X}}f(\pmb{X})= \frac{\partial f(\pmb{X})}{\partial \pmb{X}^\mathrm{T}}= \begin{bmatrix} \frac{\partial f(\pmb{X})}{\partial x_{11}} & \cdots & \frac{\partial f(\pmb{X})}{\partial x_{m1}} \\ \vdots & \ddots & \vdots \\ \frac{\partial f(\pmb{X})}{\partial x_{1n}} & \cdots & \frac{\partial f(\pmb{X})}{\partial x_{mn}} \end{bmatrix}$$

可以看到，给出的求导结果排布仍然和转置后的分母保持一致。$\mathrm{D}_{\pmb{X}}f(\pmb{X})$即称为实值标量函数$f(\pmb{X})$关于矩阵变元$\pmb{X}$的Jacobian矩阵。

事实上，基于将矩阵向量化，还可以给出有关矩阵求导的另一种定义

$$\mathrm{D}_{\mathrm{vec}\pmb{X}}f(\pmb{X})=\frac{\partial f(\pmb{X})}{\partial \mathrm{vec}^\mathrm{T}(\pmb{X})}=\left[\frac{\partial f(\pmb{X})}{\partial x_{11}},\cdots,\frac{\partial f(\pmb{x})}{\partial x_{m1}},\cdots,\frac{\partial f(\pmb{X})}{\partial x_{1n}},\cdots,\frac{\partial f(\pmb{x})}{\partial x_{mn}}\right]$$

这里$\mathrm{vec^{T}}(\pmb{X})$是指先将$\pmb{X}$列向量化后再转置得到行向量

$\mathrm{D_{vec}}_{\pmb{X}}f(\pmb{X})$即称为实值标量函数$f(\pmb{X})$关于矩阵变元$\pmb{X}$的行偏导向量。

上述两种结果有如下关系

$$\mathrm{D_{vec}}_{\pmb{X}}f(\pmb{X})=\mathrm{rvec}(\mathrm{D}_{\pmb{X}}f(\pmb{X}))=(\mathrm{vec}(\mathrm{D}^{\mathrm{T}}_{\pmb{X}}f(\pmb{X})))^{\mathrm{T}}$$

向量对向量求导

我们已经得到了标量函数对向量的求导方式，要进一步推广至向量，一种很自然的想法是对向量的每个分量分别求导即可，并且我们仍然延续前述定义对分母进行转置，于是可以得到下面的定义

$$\mathrm{D}_{\pmb{x}}\pmb{f}(\pmb{x})=\frac{\partial \pmb{f}(\pmb{x})}{\partial \pmb{x}^\mathrm{T}}= \begin{bmatrix} \frac{\partial f_1(\pmb{x})}{\partial \pmb{x}} \\ \vdots \\ \frac{\partial f_p(\pmb{x})}{\partial \pmb{x}} \\ \end{bmatrix}= \begin{bmatrix} \frac{\partial f_1(\pmb{x})}{\partial x_1} & \cdots & \frac{\partial f_1(\pmb{x})}{\partial x_m} \\ \vdots & \ddots & \vdots \\ \frac{\partial f_p(\pmb{x})}{\partial x_1} & \cdots & \frac{\partial f_p(\pmb{x})}{\partial x_m} \\ \end{bmatrix}$$

注意，这里相当于是列向量对行向量求导。

矩阵对矩阵求导

矩阵对矩阵求导的情况比较复杂，直观上想会有很多看似合理的结果排布方式。但并不是随意规定一种排布就可以的，它们很可能导致计算时不能推出正确的结果。

这里给出一种好的定义

• 首先将$p\times q$矩阵函数$F(\pmb{X})$列向量化得到$pq\times 1$的列向量

  $$\mathrm{vec}(F(\pmb{X}))=\left[f_{11}(\pmb{X}),\cdots,f_{p1}(\pmb{X}),\cdots,f_{1q}(\pmb{X}),\cdots,f_{pq}(\pmb{X})\right]^{\mathrm{T}}$$

• 然后让$\mathrm{vec}(F(\pmb{X}))$对矩阵变元$\pmb{X}$的列向量化的转置，即$\mathrm{vec}^{\mathrm{T}}(\pmb{X})$求导，就可以得到$pq\times mn$维Jacobian矩阵

  $$\begin{align} \mathrm{D}_{\pmb{X}}\pmb{F}(\pmb{X}) = \frac{\partial\pmb{F}(\pmb{X})}{\partial \pmb{X}^\mathrm{T}} \overset{\mathrm{def}}{=} \frac{\partial \mathrm{vec}(\pmb{F}(\pmb{X}))}{\partial \mathrm{vec}^{\mathrm{T}}(\pmb{X})} = \begin{bmatrix} \frac{\partial f_{11}}{\partial \mathrm{vec}^{\mathrm{T}}(\pmb{X})} \\ \vdots \\ \frac{\partial f_{p1}}{\partial \mathrm{vec}^{\mathrm{T}}(\pmb{X})} \\ \vdots \\ \frac{\partial f_{1q}}{\partial \mathrm{vec}^{\mathrm{T}}(\pmb{X})} \\ \vdots \\ \frac{\partial f_{pq}}{\partial \mathrm{vec}^{\mathrm{T}}(\pmb{X})} \\ \end{bmatrix} = \begin{bmatrix} \frac{\partial f_{11}}{\partial x_{11}} & \cdots & \frac{\partial f_{11}}{\partial x_{m1}} & \cdots & \frac{\partial f_{11}}{\partial x_{1n}} & \cdots & \frac{\partial f_{11}}{\partial x_{mn}} \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ \frac{\partial f_{p1}}{\partial x_{11}} & \cdots & \frac{\partial f_{p1}}{\partial x_{m1}} & \cdots & \frac{\partial f_{p1}}{\partial x_{1n}} & \cdots & \frac{\partial f_{p1}}{\partial x_{mn}} \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ \frac{\partial f_{1q}}{\partial x_{11}} & \cdots & \frac{\partial f_{1q}}{\partial x_{m1}} & \cdots & \frac{\partial f_{1q}}{\partial x_{1n}} & \cdots & \frac{\partial f_{1q}}{\partial x_{mn}} \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ \frac{\partial f_{pq}}{\partial x_{11}} & \cdots & \frac{\partial f_{pq}}{\partial x_{m1}} & \cdots & \frac{\partial f_{pq}}{\partial x_{1n}} & \cdots & \frac{\partial f_{pq}}{\partial x_{mn}} \end{bmatrix} \end{align}$$

总结

对于此种布局下的矩阵求导流程总结如下

• 变元（分母）需要进行转置，即列向量应当转置为行向量，为保持一致性，矩阵变元也要进行转置
• 若为向量或矩阵函数，则首先应将分子展开，即让每个分量（应该是标量函数）分别对变元求导，此时展开的排布和分子保持一致
• 按照标量对矩阵的求导规则对每个分量进行运算，将运算所得结果放到原位置上即可

梯度矩阵

采用列向量形式定义的偏导算子成为列向量偏导算子，习惯上称为梯度算子

$m\times 1$列向量梯度算子定义为

$$\nabla_{\pmb{x}}\overset{\mathrm{def}}{=}\frac{\partial}{\partial \pmb{x}}=\left[\frac{\partial}{\partial x_1},\cdots,\frac{\partial}{\partial x_m}\right]^{\mathrm{T}}$$

事实上，梯度矩阵和Jacobian矩阵的定义方式几乎完全相同，区别只在于梯度算子采用列向量形式定义，也就是说分母没有进行转置；在最终得到的求导结果上，梯度矩阵和Jacobian矩阵也只差一个转置的关系。

具体公式如下

$$\nabla_{\pmb{X}}f(\pmb{X})=\mathrm{D}_{\pmb{X}}^{\mathrm{T}}f(\pmb{X}) \\ \nabla_{\mathrm{vec}\pmb{X}}f(\pmb{X})= \mathrm{vec}(\nabla_{\pmb{X}}f(\pmb{X})) \\ \nabla_{\pmb{X}}\pmb{F}(\pmb{X})=\mathrm{D}_{\pmb{X}}^{\mathrm{T}}\pmb{F}(\pmb{X})$$

两种运算规则各有各自的应用场景，在不同的领域，可能更加“自然”的选择是不同的。在很多工程问题中，梯度矩阵就比Jacobian矩阵显得更加自然。

偏导和梯度计算

性质和法则

在计算以向量或者矩阵为变元的实值函数的偏导时，有一个基本假设：

独立性基本假设 假定向量或矩阵变元本身无任何特殊结构，即向量或矩阵的各元素之间是独立的。用数学公式可以表示为

$$\frac{\partial x_i}{\partial x_j} = \delta_{ij}= \left\{ \begin{aligned} 1,\quad & i=j \\ 0,\quad & otherwise \end{aligned} \right. \\ \frac{\partial x_{kl}}{\partial x_{ij}} = \delta_{ki}\delta_{lj}= \left\{ \begin{aligned} 1,\quad & (k,l)=(i,j) \\ 0,\quad & otherwise \end{aligned} \right.$$

而实值函数对于矩阵变元的梯度计算法则如下：

• 若$f(\pmb{X})=c$为常数，则梯度$\frac{\partial c}{\partial\pmb{X}}=O_{m\times n}$

• 线性法则

  $$\frac{\partial [c_1 f(\pmb{X}) + c_2 g(\pmb{X})]}{\partial \pmb{X}}= c_1\frac{\partial f(\pmb{X})}{\partial \pmb{X}}+c_2\frac{\partial g(\pmb{X})}{\partial \pmb{X}}$$

• 乘积法则

  $$\frac{\partial [f(\pmb{X})g(\pmb{X})]}{\partial \pmb{X}}= g(\pmb{X})\frac{\partial f(\pmb{X})}{\partial \pmb{X}}+f(\pmb{X})\frac{\partial g(\pmb{X})}{\partial \pmb{X}}$$

• 商法则

  $$\frac{\partial [f(\pmb{X})/g(\pmb{X})]}{\partial \pmb{X}}= \frac{1}{g^2(\pmb{X})}\left[g(\pmb{X})\frac{\partial f(\pmb{X})}{\partial \pmb{X}}+f(\pmb{X})\frac{\partial g(\pmb{X})}{\partial \pmb{X}}\right]$$

• 链式法则 若$\pmb{X}$为$m\times n$矩阵，且$y=f(\pmb{X})$和$g(y)$分别是以矩阵$\pmb{X}$和标量$y$为变元的实函数，则

  $$\frac{\partial g(f(\pmb{X}))}{\partial \pmb{X}}= \frac{\mathrm{d} g(y)}{\mathrm{d}y}\frac{\partial f(\pmb{X})}{\partial \pmb{X}}$$

  推而广之，若记$g(\pmb{F}(\pmb{X}))=g(\pmb{F})$，其中$\pmb{F}\in\mathbb{R}^{p\times q}$，则链式法则为

  $$\left[\frac{\partial g(\pmb{F})}{\partial \pmb{X}}\right]_{ij}= \frac{\partial g(\pmb{F})}{\partial x_{ij}}= \sum_{k=1}^p\sum_{l=1}^q\frac{\partial g(\pmb{F})}{\partial f_{kl}}\frac{\partial f_{kl}}{\partial x_{ij}}$$

计算实例

1. $f(\pmb{x})=\pmb{x}^{\mathrm{T}}\pmb{Ax}$

   $$\left[\frac{\partial\pmb{x}^{\mathrm{T}}\pmb{Ax}}{\partial\pmb{x}^{\mathrm{T}}}\right]_i=\frac{\partial}{\partial\pmb{x}^{\mathrm{T}}}\sum_{k=1}^{n}\sum_{l=1}^{n}a_{kl}x_kx_l=\sum_{k=1}^{n}a_{ki}x_k+\sum_{l=1}^{n}a_{il}x_l$$

   从而有

   $$\mathrm{D}f(\pmb{x})=\pmb{x}^{\mathrm{T}}\pmb{A}+\pmb{x}^{\mathrm{T}}\pmb{A}^{\mathrm{T}}=\pmb{x}^{\mathrm{T}}(\pmb{A}+\pmb{A}^{\mathrm{T}}) \\ \nabla f(\pmb{x})=(\pmb{A}^{\mathrm{T}}+\pmb{A})\pmb{x}$$

2. $f(\pmb{X})=\pmb{a}^{\mathrm{T}}\pmb{XX}^{\mathrm{T}}\pmb{b}$

   $$\pmb{a}^{\mathrm{T}}\pmb{XX}^{\mathrm{T}}\pmb{b}=\sum_{k=1}^m\sum_{l=1}^ma_k\left(\sum_{p=1}^n x_{kp}x_{lp} \right)b_l$$

   从而有

   $$\mathrm{D}f(\pmb{x})=\pmb{X}^{\mathrm{T}}(\pmb{ba}^{\mathrm{T}}+\pmb{ab}^{\mathrm{T}}) \\ \nabla f(\pmb{x})=(\pmb{ab}^{\mathrm{T}}+\pmb{ba}^{\mathrm{T}})\pmb{X}$$

使用类似的方法，可以按照定义得到下表：

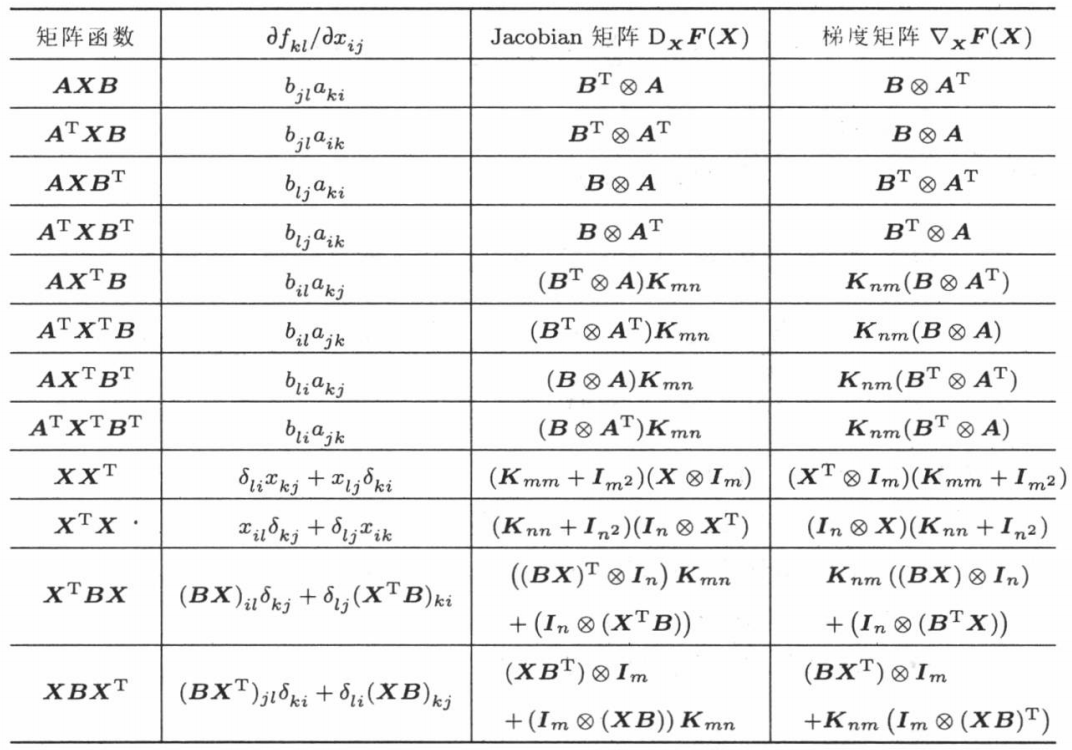
其中$\otimes$是克罗内克积，$K_{mn}$是交换矩阵

简单结论

$\pmb{A},\pmb{B},\pmb{X},\pmb{Y}$都是矩阵，且有$z=f(\pmb{Y})$，$\pmb{Y}=\pmb{AX}+\pmb{B}$

利用前述链式法则的结论，可以使用定义法得到：

$$\frac{\partial z}{\partial\pmb{X}}=\pmb{A}^{\mathrm{T}}\frac{\partial z}{\partial\pmb{Y}}$$

若条件改为$z=f(\pmb{Y})$，$\pmb{Y}=\pmb{XA}+\pmb{B}$，则有

$$\frac{\partial z}{\partial\pmb{X}}=\frac{\partial z}{\partial\pmb{Y}}\pmb{A}^{\mathrm{T}}$$

这个结论在求解很多优化问题的时候十分方便。

参考

机器学习中的矩阵向量求导(四) 矩阵向量求导链式法则 - 刘建平Pinard - 博客园 (cnblogs.com)

《矩阵分析与应用》张贤达